I’ll review in this post one of the most important notions of equivalence of behavior used in Computer Science: Bisimilarity.

Actually, “behavior” is a very deep word, and it is likely that one can not give a precise mathematical definition of what it means. But in a restricted context, there’s such definition and its surprising degree of simplicity is an indication of how fundamental it is.

Consider a computer system. Think of a keyboard and a screen. You can interact with this system by typing some orders and reading the output from there screen. Certainly, not all “commands” or actions will be available at every moment; it might even be the case that the system deadlocks and refuses to accept more actions. We’ll abstract from particular details and consider that our computer system consists of an internal set of states $S$ (e.g. the circuitry), a set of actions $L$ and a family of binary relations $\{R_a \subseteq S\times S: a\in L\}$ indexed by $L$. (We can encode both input and output using these actions.) The structure $\lb S, \{R_a : a\in L\}\rb$ is called Kripke frame in the logic literature and labelled transition system in CS.

$\newcommand{\trans}[1]{\stackrel{#1}{\to}}\newcommand{\modal}[1]{\langle #1 \rangle} \newcommand{\caja}[1]{[#1]}$So, in actual user experience, one rarely interacts with the state space but knows what actions are available and might execute one of them. A bit more formally, at every moment the system stands on a particular state $s\in S$ and the user sees the set $\{a\in L : \exists s’ ( s\trans{a}s’)\}$ of available actions. Less formally, the outer appearance of the system is that of a black box with buttons labelled by $L$, and at each moment some of them are blocked and some other can be pressed.

A Kripke frame.

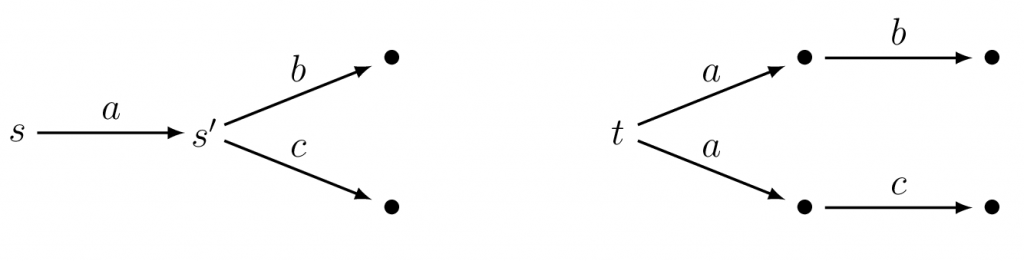
The user may choose any of the available actions, say $a$, and “press the button” corresponding to it. The system evolves to some state $s’$ such that $s\trans{a}s’$ and this leaves a new configuration of available buttons to which the user may react. For instance, standing on $t$ of the system depicted above, there are two possibilities for the next state after choosing $a$, and the user can’t decide to which of them the system will proceed, though in this example she might tell the outcome because the new set of available actions is different in each case.

When two such systems behave the same? An intuitive response would be that two users interacting with both systems (and with knowledge of what the other user can or can’t do) can not distinguish them. To formalize this notion, it’s more convenient to compare two states $s$ and $t$ of one system and try to express when the system behaves the same when starting at either of those states.

Definition. A bisimulation on a Kripke frame $S$ is a binary relation $R\subseteq S\times S$ such that for every $s$ and $t$ with $s\rr t$ we have:

1) If $s\trans{a}s’$, then there exists $t’$ with $s’\rr t’$ and $t\trans{a}t’$; and

2) if $t\trans{a}t’$ then there exists $s’$ with $s’\rr t’$ and $s\trans{a}s’$.

Two states $s$ and $t$ are bisimilar if there exists a bisimulation $R$ such that $s\rr t$.

With this definition, it is easy to see intuitively that states $s$ and $t$ in the Kripke frame above are not bisimilar. Every time a user starts at $s$ and presses the button $a$, both actions $b$ and $c$ will become available. But this is not the case with $t$.

The relation of bisimilarity can be characterized by using modal logic, and in a subsequent post I’ll describe this logic briefly and some research I did concerning it.